Example: Model Predictive Control (MPC)
This example, from control systems, shows a typical model predictive control problem. See the paper by Mattingley, Wang and Boyd for some detailed examples of MPC with CVXGEN.
Optimization problem
We will model the optimization problem
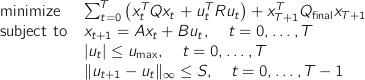
with optimization variables
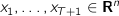 (state variables)
(state variables)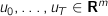 (input variables)
(input variables)
and parameters
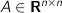 (dynamics matrix)
(dynamics matrix)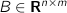 (transfer matrix)
(transfer matrix)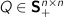 (state cost)
(state cost)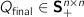 (final state cost)
(final state cost)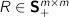 (input cost)
(input cost)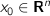 (initial state)
(initial state)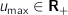 (amplitude limit)
(amplitude limit)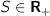 (slew rate limit)
(slew rate limit)
CVXGEN code
dimensions
m = 2 # inputs.
n = 5 # states.
T = 10 # horizon.
end
parameters
A (n,n) # dynamics matrix.
B (n,m) # transfer matrix.
Q (n,n) psd # state cost.
Q_final (n,n) psd # final state cost.
R (m,m) psd # input cost.
x[0] (n) # initial state.
u_max nonnegative # amplitude limit.
S nonnegative # slew rate limit.
end
variables
x[t] (n), t=1..T+1 # state.
u[t] (m), t=0..T # input.
end
minimize
sum[t=0..T](quad(x[t], Q) + quad(u[t], R)) + quad(x[T+1], Q_final)
subject to
x[t+1] == A*x[t] + B*u[t], t=0..T # dynamics constraints.
abs(u[t]) <= u_max, t=0..T # maximum input box constraint.
norminf(u[t+1] - u[t]) <= S, t=0..T-1 # slew rate constraint.
end
m = 2 # inputs.
n = 5 # states.
T = 10 # horizon.
end
parameters
A (n,n) # dynamics matrix.
B (n,m) # transfer matrix.
Q (n,n) psd # state cost.
Q_final (n,n) psd # final state cost.
R (m,m) psd # input cost.
x[0] (n) # initial state.
u_max nonnegative # amplitude limit.
S nonnegative # slew rate limit.
end
variables
x[t] (n), t=1..T+1 # state.
u[t] (m), t=0..T # input.
end
minimize
sum[t=0..T](quad(x[t], Q) + quad(u[t], R)) + quad(x[T+1], Q_final)
subject to
x[t+1] == A*x[t] + B*u[t], t=0..T # dynamics constraints.
abs(u[t]) <= u_max, t=0..T # maximum input box constraint.
norminf(u[t+1] - u[t]) <= S, t=0..T-1 # slew rate constraint.
end