Functions
Parameters, variables, numbers and dimensions can be used with functions, to create expressions. You may use expressions as function arguments, where supported by the relevant convex calculus.
Functions available in the objective and constraints
Assuming appropriate convexity rules, these functions may be used in the objective and in the constraints. Here are some examples of available functions, assuming previously defined symbols and appropriate dimensions:
- abs(x)
elementwise absolute value
- max(x)
vector maximum (scalar result; maximum value of the entries of x)
- min(x)
vector minimum
- max(x, y)
elementwise multi-argument maximum (vector result; third entry, say, is the larger of
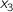and 
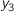)- norm_1(y)
1-norm of y
- norm_inf(y)
infinity-norm of y
- sum(x)
vector summation (equal to
)- sum[i=1..5](z[i])
summation of a scalar indexed variable (equal to
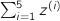)- pos(x)
elementwise positive part
- neg(x)
elementwise negative part (always gives a nonnegative number; equivalent to max(-x, 0))
Functions available as affine objective terms only
These functions can only be used as affine terms in the objective.
- square(y)
elementwise squaring of entries of a vector
- quad(x, Q)
quadratic form,
. More details below.
Quadratic forms and squared variables may only appear in the objective. This
is necessary so the problem can be transformed to a QP. While their arguments
can involve other expressions (subject to valid convexity
rules), they can only appear as affine terms.
Quadratic forms quad(x, Q), say, must have the parameter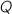 
marked as either
psd (for a convex expression) or nsd (concave). You may also use the form
quad(x), which is equal to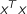 
, and equivalent to sum(square(x)).