The solver generated by CVXGEN does not explicitly handle infeasible or unbounded problems. In both cases, the solver will perform settings.max_iters steps, and terminate with work.converged == 0. This is by design.
Handling infeasibility
If you wish to avoid infeasibility altogether, change your model so it is always
feasible. One method is to replace
constraints with penalty terms for constraint violation. For example, instead of
an equality constraint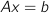 
, you could add a penalty term to the objective
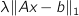, with 
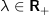(in CVXGEN,
lambda*norm_1(A*x - b)). This term is the sum of the absolute value of the
constraint violations. Choose 
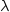sufficiently large that the equality
constraint is seldom violated. (The required value is application dependent.)
For an inequality constraint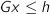 
, add a penalty term to the objective
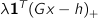(in CVXGEN, lambda*sum(pos(G*x - h))). This
term is the sum of constraint violations. Again, choose 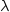sufficiently
large that the inequality constraint is seldom violated.
Using a phase I method
For total control over the behavior of your solver when no feasible point is
available, consider creating an additional solver. Here, you would
describe a second problem where the original constraints are replaced with
constraint violation terms (as described above). This solver then provides a way
to choose a point that is a compromise between feasibility and optimality in the
original formulation. See Boyd and
Vandenberghe, 
11.4, for some details and examples.
Here you might solve problems first with the phase I method, then, if the problem is feasible and bounded, use your original CVXGEN solver. Alternatively, you might use the original solver first, then upon failure to converge, switch to the alternative ‘phase I’ solver.
Handling unboundedness
To avoid unbounded problems, add additional constraints; perhaps lower and upper bounds on some or all variables. Make these sufficiently large that they do not affect ‘normal’ solution. You could then check the tightness of these constraints to determine solution behavior.