CVXGEN: Code Generation for Convex Optimization

Example: Portfolio optimization

This example, from finance, is a basic portfolio optimization problem. For some more details, see Boyd and Vandenberghe, 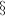4.6.3.

Optimization problem

We are given the parameters

$alpha in mathbf{R}^n$ (mean returns)
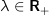$lambda in mathbf{R}_+$ (risk aversion parameter)
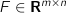$F in mathbf{R}^{m times n}$ (factor exposure matrix)
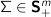$Sigma in mathbf{S}^m_+$ (factor covariance matrix)
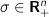$sigma in mathbf{R}^n_+$ (idiosyncratic or asset-specific variance)
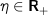$eta in mathbf{R}_+$ (leverage limit)

and wish to choose asset weights

$w in mathbf{R}_n$

to minimize our risk-adjusted mean return, subject to a budget constraint and a limit on our total short position.

Thus, we have the optimization problem

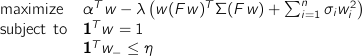
$begin{array}{ll} mbox{maximize} & alpha^T w - lambdaleft( w(Fw)^T Sigma (Fw) + sum_{i=1}^n sigma_i w_i^2 right) mbox{subject to} & mathbf{1}^T w = 1 & mathbf{1}^T w_- leq eta end{array}$

CVXGEN code

dimensions
  n = 50  # assets.
  m = 10  # factors.
end

parameters
  alpha (n)  # vector of mean returns.
  lambda positive  # risk aversion.
  sigma (n) positive  # idiosyncratic (asset-specific) variance.
  eta positive  # limit on total short position.
  F (m,n)  # factor exposure matrix.
  Sigma (m,m) psd  # factor covariance matrix.
end

variables
  w (n)  # asset weights.
end

maximize
  alpha'*w - lambda*(quad(F*w, Sigma) + sigma'*square(w))  # risk adjusted mean return.
subject to
  sum(w) == 1  # budget constraint.
  sum(neg(w)) <= eta  # limit on total short position.
end